"Tubes 201" - How Vacuum Tubes Really Work
Copyright © 2003, John Harper
Table of Contents |
Reassurance for the Math Averse There are lots of equations in this article. Be assured, if you don't like math, you can skip them. The text tells you the important things that the equations mean. Of course, if you're happy with math, you'll get more from this article. (And there isn't any real math, i.e derivations of things). |
Everyone knows how a tube works. Current passing through the filament heats it up so that it gives off electrons. These, being negatively charged, are attracted to the positive plate. A grid of wires between the filament (or cathode) and the plate is negative, which repels the electrons and hence controls the current to the plate. For many purposes that’s all you really need to know. This article looks beyond the basics, into what makes a tube behave the way it does.
As a start, let’s recap the well-known properties of tubes, which will probably be familiar to most people reading this article. We will focus on the use of tubes for audio and will look mainly at triodes, with a look later at multi-grid tubes for audio.
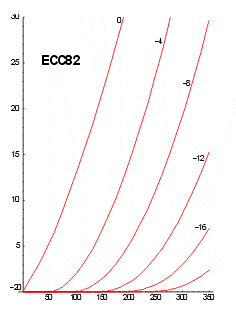
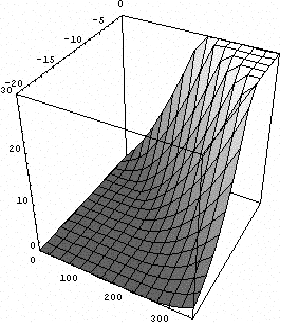
The behavior of a triode is fully described by its plate curves, as shown in Figure 1. These show the plate current as a function of plate voltage (on the horizontal axis) and the grid voltage, becoming more negative as we move to the right of the family of curves. The curves for audio tubes generally only show negative grid voltage and positive plate voltage, although it is common to operate transmitting tubes with positive grids, and it is even possible (though rarely useful) to operate with a negative plate. These curves are just a way to represent a three-dimensional surface on the printed page, and in the old days people would even build models from plaster to represent this (e.g. in [Chaff33]). Nowadays we can just ask the computer to draw it for us, as shown in Figure 2. Mathematically, this is a representation of a function which takes two arguments (grid voltage and plate voltage) and gives the plate current as its result. The standard texts (e.g. [Lang53] show how to use these curves to establish the operating conditions for a tube.
 |
 |
| Figure 1: Plate curves for typical triode | Figure 2: Surface representation of triode characteristics |
There are other ways to represent the same function. For example, we can draw the “transfer characteristics”, which show plate current as a function of grid voltage, with different curves in the family for different plate voltages. It is also possible to draw curves which show derivatives, such as the values of plate resistance and mutual conductance under different conditions. However these are not different characteristics, just different ways of looking at the same data.
One thing that leaps out is that the plate curves are just that - curves. In fact an ideal amplifying device, at least for audio, would show parallel, equally-spaced straight lines rather than curves. Unfortunately no real-world amplifying device can do this, since they all depend on physical phenomena that result in more complex transfer functions. Incidentally the obsession with linearity is somewhat peculiar to the world of audio. In other branches of electronics, such as RF and video, linearity is not so dramatically important since reasonable non-linearity can be filtered out either electronically (e.g. by tuned circuits) or by the receiving device (e.g. the eye). Only the ear can detect such tiny traces of non-linearity.
The plate curves follow quite closely a 3/2 power law, in which the current increases as a function of the 3/2 power of either the grid or the plate voltage. This is especially true at high currents and in the lower (closer to zero) range of grid voltage. While this is not linear, it is closer to linearity than any solid-state amplifying device, which is the main reason why tube amplifiers are nowadays often considered (and certainly by most of you who will be reading this) to be sonically superior. At low currents, especially as the grid becomes more negative, the 3/2 power law no longer applies and the plate curves “tuck under” very noticeably. The curves are not equally-spaced, even at high currents, but rather get closer together as current increases. All of this is causes extra non-linearity and distortion. This is more true for some tubes than for others, and later on we will look at some of the reasons.
In the sections which follow we take a look at the reality of tube design, construction and operation, which will explain why tubes behave the way they do. On the way we will explode a few popular myths.
Underlying all tube operation is the fact that any metal is continuously emitting electrons. Both the number and the speed with which they are emitted increases very strongly with temperature, although in fact emission takes place at anything above absolute zero (-273°C). To understood emission, we have to look at what is going on inside the body of the metal. In any metal, there are one or two electrons that can easily be detached from an atom, so that inside the solid metal there is a kind of sea of electrons floating around independently of any particular atom. The latter are fixed in place inside the crystal structure and do not move about at all, although they vibrate in place. This sea of electrons is common to all metals, and indeed is really the defining characteristic of a metal and explains many of their familiar properties such as electrical conductivity and the fact that they are shiny.
Since the electrons are not attached to any particular atom, they move about constantly, very much like the molecules in a gas. The average speed of the electrons increases with temperature, but because they are constantly bouncing off of the atoms and each other they do not all have the same speed but rather obey a statistical distribution law.
If an electron happens to be going towards the surface of the metal, then it will naturally tend to fly right out through the surface. However there are powerful forces trying to stop it, for the simple reason that there are positively charged metal atoms inside (because they have lost one or two electrons to the “electron sea”) and none outside. Thus an electron approaching the surface is slowed down, and only those having enough energy can escape. The amount of energy required is called the “work function”, and varies for different metals.
This is a convenient point to say how electron energy is measured. First of all, the energy of an electron corresponds directly to its speed. This follows the same law for kinetic energy as anything else, such as a car:
| where: | E = energy m = mass V = velocity |
In this case, m is the mass of an electron, which is about 10-30 kg. Energy is normally measured in Joules, but for electrons this is impracticably huge. Instead we use “electron Volts” (eV). One eV is the energy that an electron acquires when it is accelerated through a potential field of one Volt. It is about 10-19 Joules, and corresponds to a speed of about 800,000 meters/sec.
The work function of a metal is expressed in eV. For tungsten, it is about 4.5eV. Any electron having less energy than this will not manage to escape, but will be turned around by the electric field close to the surface and will return into the body of the metal.
The electrons escaping from the metal correspond to an electric current, and this current is given by Dushmann’s Equation:
| where: | I0 = emitted current A = a constant, 120.4 A/cm2 T = temperature expressed in°K (i.e. °C + 273) w = work function of emitting metal e = 2.71828… |
The striking thing about this equation is the exponential element, which means that emission increases very rapidly with temperature. Figure 3 shows the emission of a tungsten filament as a function of temperature. Even a small percentage change in temperature results in a big change in the emitted current. For an oxide-coated cathode under typical operating conditions, a 10% increase in temeprature increases emission by about a factor of 3.
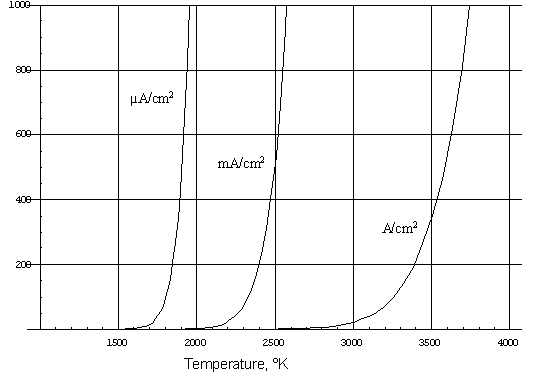 |
| Figure 3: Electron emission as a function of temperature |
The electrons that do manage to escape have the same distribution of energy as they did inside the body of the metal. Some of them flop exhaustedly from the surface, while others still have considerable velocity. This becomes important when examining the behavior of the tube. The distribution of energy (and hence speed) obeys the equation:
| where: | p =proportion of all electrons having energy greater
than V qe = electron charge, 1.602·10-19 Coulomb k = Boltzmann’s constant, 1.38·10-23 Watt-Sec T = temperature expressed in °K (i.e. °C + 273) e = 2.71828… |
It is not a coincidence that the exponential element here closely resembles that in Dushmann’s equation. Figure 4 shows this distribution graphically. The great majority of electrons have low energy levels, and the average for an oxide cathode is only about 0.1eV, but there is no upper limit on the energy that a single electron may have. For example, about one electron in a billion is emitted with an energy greater than 1eV.
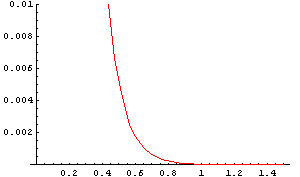 |
| Figure 4: Electron velocity distribution: proportion of emitted electrons having given energy |
Early tubes used solid tungsten filaments. Tungsten has a high work function, and there are other metals which are much more suitable in this respect (for example caesium, whose work function is only 1.6eV). However tungsten has the great advantage of a high melting point - other metals would melt long before they gave adequate emission. A tungsten filament has to be operated at about 2700°C, which is the same as a light bulb. The amount of heat thrown out by any hot object increases with the fourth power of its temperature, which means that a great deal of power (i.e. filament current) is required to replace this lost heat and remain at this temperature.
It was fairly soon discovered that the addition of a small amount of the obscure element thorium (about 1%) to tungsten greatly reduces its work function, to about 2.6eV, allowing filament operation at around 1900°C. This reduces the required power by about a factor of four. Such tubes were called “dull emitters”, because compared to a tungsten filament (or a light bulb) they were much less bright.
Later it was found that a surface coating of barium oxide (or a mixture of barium and strontium oxides) gave even better results. This is because the oxide is no longer a metal, and the energetic electrons within the body of the filament can escape through the oxide layer at much lower velocity. In fact, the oxide layer is a n-type semiconductor, i.e. one having an excess of electrons, and its behavior is due to this. Oxide filaments have a work function of about 1.1eV, and can be operated at around 700°C. It is this oxide coating which makes filaments and cathodes appear white. There are however disadvantages. The oxide coating is mechanically fragile, and can be damaged as a result of gas in the tube or by vibration or shock. This is why high voltage tubes (such as the 211 and 845) still use thoriated tungsten. It is also relatively volatile, and slowly evaporates from the surface of the filament from where it is deposited in undesirable places such as the grid wires. Emission from an oxide surface is much more complex, in physical terms, than from a pure metal, although it does still essentially follow Dushmann’s equation. Overall, though, the advantages of oxide-coated filaments and cathodes for small-signal tubes are overwhelming, and no other materials have been used since the 1930s.
Electrons within the body of the cathode are travelling in all directions, and in consequence so are the ones that are emitted. It turns out that the average lateral (sideways) velocity of the electrons is about the same as their average forward velocity. It is therefore wrong to think of them all travelling along the shortest straight line from the cathode towards the plate.
There are many different ways that a filament (or cathode), a grid and a plate can be constructed and put together, and many of them have been tried over the years. From here on, we will concentrate mainly on indirectly heated tubes, having a distinct heater and cathode, rather than filamentary tubes. These appeared in the early 1930s, primarily as a way to allow the heater to operate from AC rather than DC. The only disadvantage of indirect heating is that it is less efficient, i.e. more energy input is required for operation at a given temperature. This is why tungsten and thoriated filament tubes (e.g. 211, 845, SV572) are still directly heated, due to their much higher operating temperature, and also why battery tubes were. For oxide cathodes, the best known filamentary tube in common use today is the 300B, together with a few other power types.
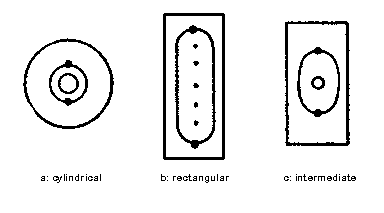 |
| Figure 5: Types of triode construction |
There are three common tube structures, shown in Figure 5. 5a shows the cylindrical structure, in which the cathode, the grid and the plate are made as three concentric cylinders. This structure has been little used since the 1930s, presumably because it is more expensive to manufacture. (An exception is rectifier diodes, which are almost invariably built like this). It does however have some theoretical properties that may account for the sonic reputation of the classic model 27 and 76 triodes, which are built this way. The grid is wound as a spiral, generally with two vertical support posts. The grid wire is rigid, and holds its shape once it has been formed into shape.
Figure 5b shows the flat structure used in power tubes such as the 6AS7 and (with a filament rather than a cathode) the 2A3 and 300B. Here the grid is also wound around two vertical supports, but in this case it is flat (although often curved outwards slightly around the cathode). Like the cylindrical structure, this lends itself readily to theoretical analysis.
Figure 5c is a compromise between the two. The grid and the plate are flat, but the cathode is a small cylinder. This is a common construction for small tubes such as the 12Ax7 family or the 6SN7. Its behavior is very close to the truly flat structure of Figure 5b. There are many variations on this; for example, the plates are often elliptical rather than rectangular as shown. Similarly, the cathode may be elliptical. Since the characteristics depend directly on the geometry, this results in less consistent operation and is therefore undesirable for audio.
The challenge for the tube designer is to get the grid as close as possible to the cathode. As we will see later, this is the principal factor affecting the mutual conductance of the tube, and for most purposes higher mutual conductance means better. However, there are problems. First of all, the slight variation in grid-cathode spacing inevitable due to manufacturing tolerances leads to indistinct characteristics, since different parts of the tube are behaving differently. Indeed, if the spacing is too close then there is a risk that the two may even come into contact, with disastrous results. Secondly, if the spacing is much less than the distance between the grid wires then the tube performance becomes difficult to predict and may even get worse. This in turn led to pressure to wind the grids from ever-finer wire at an ever-tighter pitch. Miniature tubes typically use grid wire that is less than one-thousandth of an inch thick, with a grid-cathode spacing at its closest of little more than this.
Most of the metal inside a tube is nickel, which has a number of desirable properties. First, it has a high melting point. Copper, for example, would be unsuitable because it would soften and distort. Secondly, it does not absorb a lot of gas onto its surface (the technical term for this is “adsorption”). Such adsorbed gas is gradually released into the vacuum of the tube, and it is important to minimize it. An exception to the use of nickel is the heater (or filament) which is generally made of tungsten because of the high operating temperature.
The plate is generally blackened, because a black surface radiates heat much more effectively than a lighter one. The only way that heat can be removed is by radiation, and it is this that sets the limit on the power dissipation of a tube. Power tubes have plates that include large radiating surfaces having nothing to do with their electrical function, and even small-signal tubes often have wings or corrugations that serve the same purpose.
Because of the very close clearances, and also because of the impact of tube geometry on electrical characteristics, it is vital to maintain the dimensions to very close tolerances. The metal wires that support the various electrodes are generally held apart by spacers made from mica, which is an excellent heat-resistant insulator that is also very vacuum-friendly and easy to work to precise dimensions.
The heater is inside the cathode. Since the cathode itself is small, there is little room for it and even less room for electrical insulation. A thin layer of alumina (aluminium oxide) is normally used, but at the high temperatures involved this is not a perfect insulator, and if the voltage difference is too high then it can break down altogether. This is why all tubes have a rating for the maximum voltage difference between the heater and the cathode, typically 100-200V. Exceeding this may result in insulation breakdown, and of course failure. Even at lower voltages, there is some resistive and especially capacitative coupling between the heater and the cathode.
It is a very instructive exercise to take a tube to pieces and to measure the internal dimensions. Don’t do this with a new Western Electric 300B, but take a defunct octal tube such as 6SN7 (the miniature tubes are too fiddly), break the envelope by wrapping it well in a cloth and tapping it with a hammer. (Be careful doing this, and be careful as well with the shards of broken glass afterwards. Remember that some parts are mildly poisonous, and don’t even think about doing it with transmitting tubes which can contain highly toxic beryllium). You can then gradually dismantle the electrode structure, seeing how it is put together. You will find, for example, that many tubes have tiny metal plates welded to the tops of the grid supports, whose job is to get rid of the heat generated on the grid due to grid current. (In this case of the 6AS7G, these are comparable in size to the plates themselves).
If plate voltage is applied to a cold tube, then an electric field is set up between the plate and the cathode. The voltage in this field increases linearly in the distance between the two electrodes. This is shown by the red line in Figure 6. Once the cathode is heated up and starts emitting, the electrons themselves alter the situation, because the electron carries a negative charge. Although this is very small (1.602·10-19 Coulombs), there are a lot of them, and the emitted electrons themselves contribute to the electric field in the space between the electrodes, modifying it from the straight line shown in red in Figure 6. The green line shows the effect using a simple analysis, ignoring initial electron velocity (Child's Law), while the blue line shows the true state of affairs when initial electron velocity is considered.
The term space charge is used to refer to the charge due to the electrons occupying the inter-electrode space. The space charge plays a crucial role in controlling the flow of current, which is at the heart of the controlled amplifying action of the vacuum tube. There are several myths and misunderstandings concerning space charge. It is often implied that it exists only in the immediate region of the cathode, and there are references to the “space charge region”. It is true that the space charge in this region has particular importance, as we shall see later, but it is present in the whole inter-electrode space. Another source of confusion is the “space charge tubes” which were developed in the 1950s, for use in car radios. To allow them to operate effectively on the 12V supply in the car, without needing a higher voltage, they used an unusual configuration of grids to limit the reduction in plate current due to the space charge. These are now of interest only to collectors.
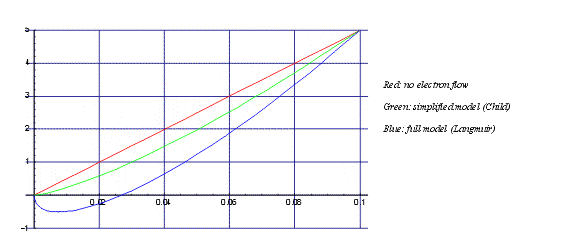 |
| Figure 6: Charge distribution between cathode and plate |
The number of electrons depends on the current flow - the higher the current, the greater the number of electrons and therefore the greater the charge. Since the cathode feels the influence of the plate through the negatively-charged electrons between them, the increasing current reduces the attractive force of the plate until the two reach a balance. At this point of balance, the effective field at the surface of the cathode is reduced to zero. Moving away from the cathode, the electrons accelerate. The accelerating electrons spread out, just like cars on a freeway moving away from a traffic jam, reducing the space charge so that the field increases. This is illustrated by the green line in Figure 6, which shows what happens inside a tube when current is flowing under normal operating conditions (under this analysis).
The mathematics of this is beyond the scope of this article, but it is relatively straightforward to obtain the Child-Langmuir law (sometimes referred to simply as Child’s law), as it applies to a diode:
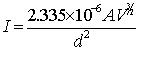 |
where: | V = plate voltage A = cathode area d = distance between cathode and plate (cm) |
This is the well-known 3/2 power law of the relationship between current and voltage. Note also the bottom of the equation: the current drops with the square of inter-electrode distance. This is why designers need to keep the physical dimensions of the tube as small as possible.
This equation (and the green line in Figure 6) is based on a simplification, that all of the electrons are emitted with zero residual energy. We have already seen that in fact they are emitted with a distribution of energy, and later on we look at the effect this has.
This law strictly applies only to infinite flat electrodes. In reality of course the electrodes are finite, but in a practical tube the effect of this is relatively minor. A similar equation applies to cylindrical electrodes, which still involves the 3/2 power of voltage, and in fact it can be shown that any electrode configuration will involve this factor.
One implication of this law is that the current flowing depends only on the strength of the field due to the plate in the immediate vicinity of the cathode. This field must be just strong enough to counter exactly the space charge set up by the resulting current. The field elsewhere serves to accelerate the electron flow but plays no role in determining its magnitude.
The current emitted by the cathode under normal conditions is far in excess of the current that passes to the plate. The emission of an oxide cathode is upwards of 0.5A/cm2. Even for a power tube, the ratio between the emitted current and the operating current is at least 10. The maximum plate current rating that appears in the specification for a tube is based mainly on considerations of heating, and in pulse operation can safely be exceeded (as it was in TV sweep circuits, for example).
If all of the emitted electrons do pass to the plate, then the operation is completely different. The plate current becomes practically independent of the plate voltage. In a triode, the grid no longer has any control over the current. This mode of operation is called thermal saturation (or just saturation), in contrast to the normal mode which is sometimes called space-charge limited. Under these conditions the full effect of the field due to the plate is felt directly at the cathode, since the space charge (which does still exist) is no longer strong enough to counter it. In fact, the current does increase a little with plate voltage, especially with oxide cathodes, because the increasing field strength can pull more electrons out of the surface of the cathode. This is called the Schottky effect. It must be stressed though that in audio, no practical vacuum tube circuit operates in saturation, even for short periods. (There are uses in other areas. One is the noise diode, which is deliberately operated with a low heater voltage so that emission is low, and saturation occurs continuously. Another is in high-current pulse switching).
Back in 1871, long before the thermionic valve was invented, Maxwell [Max71] published the first study of the effect of a grid of wires on the field between two electrodes. Making some simplifying assumptions, he showed that the electric field as seen at the cathode is equivalent to a plate voltage of:
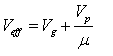 |
µ is a constant for a given electrode geometry. In other words, the actual plate voltage is divided by µ to get the effective voltage. For example, in a typical medium-µ triode under normal operating conditions, the effective voltage as seen at the cathode is only around 5V, even though the plate is at 100V or more.
Maxwell showed that µ can be calculated as follows. (More and more elaborate formulae for µ were developed throughout the life of the vacuum tube, and Maxwell's is not terribly accurate for real-life tubes).
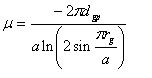 |
where: | dgp = distance from grid to plate a = distance between grid wires rg = radius of grid wires |
In non-mathematical terms, this means that µ increases directly with the distance from the grid to the plate, and with the ratio of grid wire size to separation (also called the grid pitch or shielding ratio). It also means that the value of µ is independent of the distance from the cathode to the grid. The variation of µ with cathode-plate distance is very visible. If you hold up high- and low-µ version of essentially the same tube, e.g. 6SL7 and 6SN7, or 12AX7 and 12AU7, you will see that the plate structure is much fatter in the high-µ tubes.
The assumptions that Maxwell made for his calculations were as follows:
When the last condition is true, the effect of the grid wires is seen only collectively at the cathode, with no effect from individual wires even directly under them. Figure 7 shows the field, by lines of constant potential, under varying grid potentials. It can clearly be seen that when the tube is conducting (i.e.the potential at the cathode is above zero) the field is uniform at the cathode. The effect of the individual wires falls off exponentially with the distance. At half-cutoff, the "bulge" due to the plate's field penetrating the grid is significant up to well over half-way to the cathode. This becomes significant for more modern tubes where the cathode-grid spacing is typically 60% of the grid pitch. Figure 8 shows the field in a cross-section of the tube, at a grid wire and midway between two grid wires, when no current is flowing, i.e. when there is no space charge. It shows that once past the grid, an electron is subject to the full potential gradient due to the plate voltage, but downstream of the grid this is essentially masked by the grid voltage, as predicted by Maxwell.
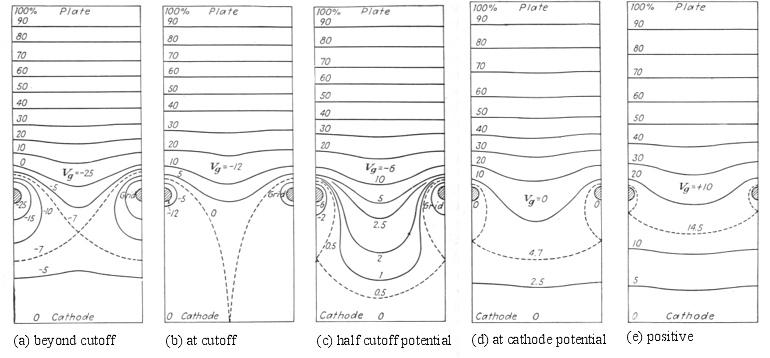 |
| Figure 7: Triode equipotentials |
|
|
| Figure 8: Section of triode electric field |
Using the effective plate voltage, we can start to calculate the current that will flow in the tube, following Child’s Law, but we also need to know the value to use for the cathode-plate distance. A good approximation is given by:
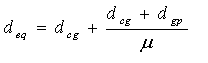 |
where: | deq = equivalent effective distance of diode plate dcg = distance from cathode to grid dgp = distance from grid to plate |
(Spangenburg [Spang48] gives a more accurate, and more complicated, formula, but the result is only slightly different). Inserting this into Child’s Law gives the complete equation for cathode current under given conditions:
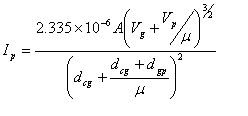 |
or | 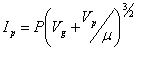 |
In this formula, everything except the grid and plate voltages is determined by the geometry of the tube’s construction, and is therefore a constant for a given tube. The factor P in the equation is called the perveance of the tube, and is the measure of the current it will pass under given conditions. It is just all of the terms from the first equation, outside the voltage term, gathered up into one variable. A high-perveance tube is therefore simply one that will carry a high current. It can be seen that there are two ways to increase the perveance, either by increasing the electrode area or by decreasing the electrode spacing. The latter is more effective, but is limited by the mechanical construction techniques and achievable tolerances. Once the closest possible spacing has been reached, the only way left is to increase the area. This is why power tubes are physically large, ultimately leading to tubes like the monster WE212A which stands 13" tall.
A triode is described essentially by three well-known so-called constants:
| Voltage amplification (µ) | As described above, the factor by which the grid reduces the effect of the plate voltage |
| Mutual conductance (Gm) | Expressed in milliamps/volt (or nowadays milliSiemens, which means the same thing) – the increase in plate current for a change in grid voltage |
| Plate resistance (rp) | The effect output resistance of the tube – for small signals, the tube is equivalent to a voltage source in series with a resistance of this value |
In fact, only two of these characteristics are required, since the three are connected by the relation:
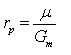 |
These constants appear in even the briefest data for a tube. Unfortunately, they are not at all constant. Figure 9 shows (for the 6SN7, a particularly linear triode) how they vary with plate current.
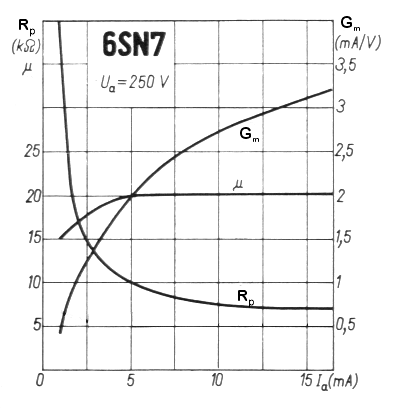 |
| Figure 9: Changes of characteristics "constants" with plate current |
It can be seen that both Gm and rp vary a great deal. In fact, this follows from Child’s Law. With a little calculus (differentiating the formula with respect to Vg) and some algebra, we arrive at the formula:
In other words, the value of Gm increases with the cube root of the plate current, and hence the value of rp decreases with the cube root of the plate current. Since Gm is a key figure of merit for a tube, the manufacturer would always want to show the highest value, whch is to say at the highest rated operating current. More typical and reasonable operating levels reduce Gm and increase rp. For the 6SN7 shown, Gm is 3.2mA/V at 16mA, but drops to 1mA/V when operating at 1.5mA. As in this case, Gm typically drops faster than the formula predicts, particularly at low currents and high negative grid voltages.
The curves also show that µ is not really constant, either. Over the range 5 – 1 mA, it drops from 20 to 15, i.e. by about 25% - and this is a particularly linear tube in this regard. Later, miniature tubes show a steady drop over the whole operating range. The explanation for this is not so simple, and indeed the classic tube texts do not give any help. Mainly it has to do with the changing shape of the electric field in the region between the cathode and the grid as the grid becomes more negative and the current drops. Especially with close electrode spacing (discussed in greater detail below), close to cut off, parts of the cathode below the grid wires are cut off while parts between the grid wires are still conducting - as can be imagined from Figure 7c. It can be shown that the parts which are still conducting have a lower value of µ. (This phenomenon is called inselbildung, German for "island effect"). Another reason, particularly important at low currents, is that the value of µ is not constant throughout the tube. Variations due to the edges of the electrode structure, grid support wires, and irregular electrode shape mean that there are places where it is higher. As current falls, these areas are the first to cut off, leaving only the lower µ regions conducting. In consequence, the average value of µ falls with the reducing current, explaining the distinct tailing off at low currents.
The derivation of Child’s Law assumes that electrons are emitted from the cathode with zero velocity, but in the description of emission we have seen that this is not the case. As shown in Figure 4, emitted electrons have a distribution of energy which falls off rapidly. This means that all of them have enough energy to move away from the cathode, creating a dense cloud of electrons just ahead of the cathode. This in turn creates a dense region of space charge, and it is this space charge which, by repelling the emitted electrons, reverses their direction and sends them back to the cathode. Only the small minority that are emitted with enough energy to penetrate this strongly-charged region are able to reach the attracting field of the plate and hence form part of the plate current.
This affects the current flow in the tube in a number of significant ways. The blue line in Figure 6 shows the electric potential in the space between the cathode and the plate (of a diode), taking into account the initial velocity. Initially this potential drops to a negative value, which then starts to rise. The minimum of the negative value forms a virtual cathode, and it is from this virtual cathode that the calculation of current flow must be taken into account. (Both the potential of the virtual cathode and its distance from the physical cathode depend on the current flow, which creates an obvious problem of circularity for computing the current.) The effect is that, firstly, the effective cathode-plate distance is less than the physical distance, and secondly, that the effective plate potential is increased. The latter is significant, considering that the effective plate potential, as seen at the cathode, is only a few volts.
Even beyond the virtual cathode, some of the electrons still have some residual energy. The effect of this is to increase the current beyond what Child’s Law predicts. The full physics of what is going on here is complex, and leads to some alarming mathematics, which were first fully worked out by Langmuir in 1923 [Lang23], and can also be found in [Dow37] and [Spang48]. Approximate formulae are shown below.
|
where: | dvc = distance from physical cathode to virtual cathode Ip = plate current T = cathode temperature (typically around 1050°K) I0 = total emitted current Vm = potential at virtual cathode Vp = plate voltage dcp = distance from cathode to plate A = cathode area |
||
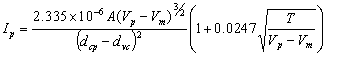 |
||||
It can be seen that evaluation of these formulae requires knowledge of the emitted current from the cathode. This is a hard quantity to measure, and in addition it decreases continuously during the life of the tube. For a new tube a typical value is around 1A/cm2, i.e. around 100 times the plate current. The key equation above is the bottom one, which gives the plate current in terms of potentials. It is rather frightening, so start with the left part. This simply Child's law, as seen earlier, with a correction for the potential and distance of the virtual cathode. The final term is the correction for initial velocity, which at low currents represents a subsantial increase in plate current.
Substituting some typical values into these formulae shows that the reduction in effective cathode-plate separation due to initial electron velocity is around 0.1mm, while the increase in effective plate (or combined plate and grid) potential is around 0.5V. The increased current due to initial velocity is around 10-25%. These figures increase substantially as the tube gets close to cut-off, especially the distance to the virtual cathode. In fact at very low currents (say under 1mA for small-sgnal tubes) the transfer characteristic, starts to have an exponential nature. In audio terms, its behaviour starts to be more like a junction semiconductor (for the same underlying physical reasons), producing larger amounts of higher-harmonic, which is to say unpleasant, distortion.
These formulae also explain why the heater voltage has an effect on the operation of a tube, which is not explained by Child’s Law. As heater voltage is increased, two things happen. First, the emitted current is increased, thereby increasing the effective plate voltage. Second, the increased energy of the emitted electrons (due to the higher temperature) provides an additional reason why the plate current will increase. In fact, a 10% increase in heater voltage gives about a 5% increase in plate current.
Because the virtual cathode is negative with respect to the cathode, some current will flow even if the plate is at the same potential as the physical cathode. Mitchell [Mitch93] shows that a 12AU7 with 0V on both the grid and the plate passes a current of 90µA, while the 6DJ8 under the same circumstances passes 0.3mA, the latter due to the closer electrode spacing. (Anecdotally, the author had a Leak FM tuner which gave low and distorted output. Investigation showed that a broken wire meant that the first stage, an ECC85, was operating with 0V on the plate. But it was still passing a signal).
The formulae given above apply to a plane electrode structure (i.e. Figure 5b). If the electrodes are truly cylindrical (Figure 5a) then different, rather more complicated, formulae apply, but the general principle remains the same. However, there is one significant difference, which is that the distance from the true cathode to the virtual cathode (dvc) is smaller with cylindrical tubes. This may be the explanation for the reported qualities of early triodes such as the 76.
If the plate is made negative, some current will still flow. As it decreases, the virtual cathode will move further away from the physical cathode, until eventually it reaches the plate. From this point on, a different set of rules apply and the current decreases exponentially with increasingly negative plate voltage:
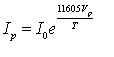 |
(Note that in this formula Vp is negative). Thus in principle the current is never reduced completely to zero, but at Vp=-1.3V it is reduced to 1µA, and at Vp=-1.9V to 1nA.
The pool of electrons in region between the physical and virtual cathodes is sometimes stated to form a reserve that can supplement the cathode’s emission during current peaks. This is a myth; these electrons have a very short lifetime before they return to the cathode, and correspond to less than 1nS of emission.
All electronic, and indeed electrical, devices produce noise. The most fundamental, and unavoidable, form of noise is called thermal noise or sometimes shot noise. It occurs because the flow of electricity is actually due to individual electrons. Even though the number of electrons is huge, there are still statistically predictable fluctuations, just like traffic on the highway. Because it is random, this noise occurs equally at all frequencies. The noise voltage developed by a simple conductor or resistor is given by:
| where: | enoise = noise voltage k = Boltzmann’s constant, 1.38·10-23 T = temperature, in ºK R = resistance Df = bandwidth |
For example a 1kW resistor at room temperature (approx. 300ºK), across the audio bandwidth from 0-20kHz, produces a noise voltage of about 0.6µV. When dealing with very small signals, such as a received radio signal or a phono pickup, this is a significant amount of noise.
Vacuum tubes produce thermal noise. They also produce noise in two other ways, called flicker noise and separation noise.
It turns out that there is a very simple way to calculate the thermal noise in a triode. The noise produced by the tube is equivalent to a resistor in series with the grid, at room temperature, whose value is given by:
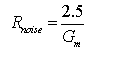 |
In other words, the noise produced by a tube is inversely proportional to Gm. This directly explains the modern interest in high Gm tubes such as the WE417A. This tube was intended for the first stages of sensitive VHF and UHF receivers, where minimum noise is a critical feature, but is also of interest for sensitive phono stages.
The second source of noise in tubes is flicker noise, also called 1/f noise which clearly describes its nature: it is noise which decreases with frequency. It is of no interest for radio work, but has obvious importance for audio since most of the noise lies in the audio band. It is particularly important for phono stages, since the RIAA correction, by attenuating higher frequencies, boosts the contribution of noise at lower frequencies.
Flicker noise is caused by variations in cathode emission due to movement of atoms within the cathode structure. In oxide-coated cathodes, it occurs primarily at the interface between the oxide layer and the base metal of the cathode, which is generally a nickel alloy. Some alloys are much better than others in this respect, showing a difference of a factor of 20 or more [Smullin59, p65]. A high silicon content increases flicker noise, but unfortunately has advantages in the manufacturing process and so tended to be widely used. The cathode alloy was chosen by each manufacturer, and does not form part of the specification of a particular tube type, which explains the wide variation about tubes from different manufacturers. Smullin [Smullin59] indicates that European manufacturers tended to use alloys which are better in this respect.
Pure tungsten filaments generate flicker noise in a different way, resulting in a noise spectrum which is 1/f 2 rather than just 1/f.
The third source of noise applies only to tetrodes and pentodes, and explains why pentodes are noisier than triodes. The presence of the positive screen grid means that some of the current (typically 10-20%) from the cathode goes to the screen grid rather than the plate. However this division of current fluctuates randomly, just as the current itself does. This very slight random variation in the plate current is called partition noise.
The effect of partition noise is to change the equivalent noise resistance from the simple formula given above to:
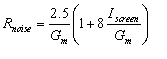 |
where: | Iscreen = screen grid current |
In practice, this results in three to five times the noise of the equivalent triode. Connecting a tetrode or pentode as a triode eliminates partition noise, since now the two current flows are recombined.
When an energetic, fast-moving electron hits a metal surface, the impact dislodges some of the other electrons and causes them to be emitted. An electron arriving at a 250V plate has an energy of 250eV, whereas the metal’s work function means that only around 4eV is required for an electron to be emitted. This phenomenon is called secondary emission, and occurs each and every time an energetic electron arrives. Under normal conditions, the plate is the most positive thing around, and these secondary electrons are simply attracted back to the plate where, having only a little energy, they are re-absorbed without provoking any further emission. This is benign and has no effect on the electrical operation of the tube, and is indeed unmeasurable.
Secondary emission only becomes a problem when the emitting surface is not the most positive thing nearby. In this case the emitted electrons are captured by the electric field and form a secondary current between the two electrodes. For example, if the grid of a triode is made positive rather than negative, and more positive than the plate, so that electrons flow directly to it, then the secondary electrons will be attracted to the grid, causing a flow of current away from the plate.
Secondary emission - or more accurately, secondary current flow - is almost never a good thing. It occurs unavoidably in the tetrode (as described below) and is the principal reason why tetrodes have been replaced by pentodes. It was exploited in photomultiplier tubes, as a way to multiply a very feeble initial current. There was also a tube in the late 1930s, the Philips’ EFP60, which used secondary emission from a target electrode as a way to increase the Gm, but it proved difficult to build predictably and was not successful. The problem is that although secondary emission can be measured for a particular metal, and in principle allowed for, in practice it is heavily affected by surface contaminants and the like. It cannot therefore be used as a reliable element of a tube’s operation.
In theory, the inside of a tube’s envelope is a vacuum. In practice, a perfect vacuum is unachievable, and a certain level of residual gas has to be accepted. The pumps that are used to evacuate tubes can typically get down to about 10-7 mm of mercury, or about 10-10 of atmospheric pressure. However once the tube is sealed, gas can still get into the space inside it. First, the glass-to-metal seals around the pins or lead-out wires are not perfect, and allow small amounts of air to pass. Secondly, a certain amount of gas is adsorbed at the surface of the metals, mica and glass inside the tube. Under the high vacuum, this gas is slowly released, particularly if the surface is raised to a high temperature. This is the main reason why allowing the plate of a tube to overheat is bad for it – it results in a sudden release of gas which interferes with the tube’s operation and can rapidly result in destruction of the cathode.
An essential part of the structure of all tubes is the getter, the silvery coating to be seen somewhere on the glass envelope. It is generally made of barium, which reacts (when hot) with gases, taking them out of circulation as soon as they appear. As the tube ages, the getter is gradually used up. Anything resulting in a serious gas leak will exhaust the getter quickly, and this can easily be seen because its appearance changes from silvery to white. In manufacture, the getter is placed inside a special container, often a small cup which can be seen attached to the internal structure close to the getter location on the envelope. Once the tube has been exhausted by a pump, and sealed, the getter is fired either by passing an electric conduction or using an induction heater, which deposits the film on the envelope.
If the vacuum is not perfect, and we have seen that it never is, then some gas molecules remain inside the tube. When an energetic electron hits such a molecule, it generally knocks one or more of the electrons out of it resulting in a positively charged ion, which is then attracted in the opposite direction from the electrons, i.e. towards the grid and the cathode. The grid is generally the most negative part of the tube, but because these ions are relatively massive they do not change direction easily and so a significant proportion of them pass through and hit the cathode. Here their energy is able to dislodge the surface atoms, particularly in oxide cathodes, which is called cathode stripping. The gradual erosion of the cathode surface is one of the principal factors limiting the life of small tubes. This is why tubes should ideally not have plate voltage applied until they are warm, since in this way the getter has a chance to deal with gas molecules which have appeared since the tube was last operated.
The chances of an individual electron colliding with a gas molecule are very small. In a new tube an electron could travel around 10 kilometers on average, before having such a collision. However, because of the large number of electrons involved in carrying the current, the number of such ionisation events is large – around one billion per second for a small tube in typical conditions, with a good vacuum (10-7 mm Hg).
Any closely-spaced conductors have a capacitance between them, and the electrodes of a tube are no exception. In a triode, the capacitance from the grid to the plate and the cathode respectively could in principle be worked out from the tube dimensions. Typical values are a few pF for each of them, for small-signal tubes. Large-signal tubes have higher values, simply because of the larger electrode areas.
There is also a capacitance between the plate and the cathode, but this is reduced by a factor equal to µ from what the normal capacitance formulae would give. Typical practical values are 0.5-1pF, but this is largely due to capacitance between the lead-out wires rather than in the electrode structure.
Finally, the very close spacing between the cathode and the heater packed inside it also results in capacitive coupling, typically around 1pF. This allows noise and RFI, in particular, to couple from the heater supply into the signal, and indeed vice versa.
The most common amplifier circuit is the common cathode, but the interelectrode capacitance causes a particular problem in this configuration at RF and even at the higher audio frequencies. As the grid voltage rises, the plate current increases and hence the plate voltage falls by an amount equal to the amplification of the circuit. But this falling voltage is capacitively coupled back into the grid, leading to the Miller Effect in which the effective value of the grid-plate capacitance, as seen by the driving circuit, is multiplied by the gain of the circuit. Whereas a value of say 4pF would have little effect, certainly for audio, the Miller Effect results in a value of several hundred pF, which cannot be ignored.
Since the grid has no physical connection to anything (as the circuit symbol shows), it is natural to think of it as being electrically isolated. In fact, this is not the case, because of the flow of electrons and ions inside the tube.
Current flow to and from the grid arises for two reasons. The most obvious is when the grid is positive, which causes it to attract electrons. Less obviously, when the grid is negative, it attracts positive ions resulting from collisions between electrons and gas molecules. These cause the grid to become less negative. It is because of this effect that the grid must never be left truly floating but must always be connected through a resistance, typically for a small tube not more than 1MW. Without this, the voltage of the grid will gradually creep up, reducing negative bias and increasing current through the tube and leading to a runaway which, at worst, will destroy it through overheating. Tube gassiness is measured, in tube testers, by measuring this small current (typically a few nA), which is in direct proportion to the amount of gas in the tube.
At the right voltage, these two currents cancel out. This normally occurs at around –0.5V (depending slightly on plate voltage), which is slightly positive relative to the virtual cathode. If the grid is simply left disconnected, it will float at this voltage.
Positive grid current is deliberately used in some cases, for example in high-µ transmitting tubes. When it occurs, Child’s Law (or the more accurate formula taking account of initial electron velocity) gives, not the plate current, but the sum of the plate and grid current. This is because total current is controlled by the field in the immediate vicinity of the cathode, which is due to the combination of the two other electrodes. To calculate the actual plate current (and hence also grid current), it is necessary to know how much of the electron stream flows to each of the two electrodes. This is given from the following formula:
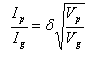 |
where: | d = current division factor |
The current division factor is slightly greater than the shielding ratio of the grid. If grid current curves are available for a tube, it is easy to determine its value from them.
Unfortunately this tidy formula only gives the value for the primary current. Once the grid is more positive than the plate, secondary emission will start to occur, resulting in a secondary current flow from the plate to the grid and reducing the effective grid current. This is, for all practical purposes, unpredictable. Depending on the tube, the secondary current may even exceed the primary current, typically at around 30-50V, resulting in a second stable voltage for a disconnected grid at the point where the primary and secondary currents exactly balance.
Positive grid current results in heating of the grid, for the same reason that the plate gets hot (i.e. due to the kinetic energy of the arriving electrons). Small tubes are not generally designed for this, but power tubes and especially tubes designed for positive grid operation have substantial dissipators attached to the grid structure. Overheating of the grid is bad for two reasons. Firstly, since it is not designed to run at a high temperature, it does not have any way to retain its tension as the metal expands. This results in changing geometry and in the worst case melting or a short to the cathode, which is instant death. Secondly, the grid is generally contaminated by oxide from the cathode, and if it gets hot then it will start to emit electrons like the cathode, resulting in a substantial secondary current.
Because Gm increases inversely with the square of the grid-cathode distance, tube designers have always been under pressure to reduce this distance. However, if it falls below the grid pitch, the design assumptions of the triode start not to apply. The field is no longer uniform at the cathode, but rather varies, becoming less negative between the grid wires. In fact, if the separation falls below 0.6 of the pitch, the Gm starts to fall again. As a result, the evolution of vacuum tube technology is marked by ever-finer grids, so that this relationship can be maintained. Fremlin [Frem39] describes the theory which applies when the grid is closer to the cathode than its pitch.
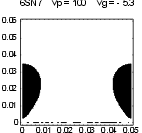
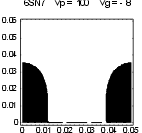
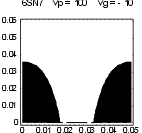
Figure 10 shows how this applies to a 6SN7, which being an older design does not have especially close spacing. At -5.3V grid potential, the whole cathode is contributing to the plate current. As the grid becomes more negative, "inselbildung" starts - the parts of the cathode directly under the grid wires are in a negative field. By -10V less than half the cathode is still contributing. At -11.4V, the whole cathode is seeing a negative potential, and the tube is truly cut off, i.e. there is no plate current. It can be shown that the effect of inselbildung is to replace the 3/2 power in Child’s Law by a 5/2 power. Thus at high currents and small grid voltage, the tube obeys a 3/2 power, but as the grid is made more negative and current reduces, this gradually turns into a 5/2 law. This is the principal reason for the “tuck under” that plate curves show at large negative grid voltages.
 |
 |
 |
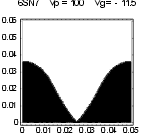 |
| Figure 10: Zero-volt potential contour as tube approaches cutoff (dimensions in cm) | |||
So far this is purely a question of proportion, and not of the absolute size of the tube. Recall however that the space charge creates a virtual cathode typically about 0.1mm ahead of the physical cathode, which further reduces the effective distance to the grid. This distance is independent of the tube geometry. It is 0.1mm whether in an early tube with 2mm from cathode to grid, or in a 1950s design where it may be 0.2mm or less - which places the grid only slightly ahead of the virtual cathode. In fact the virtual cathode is no longer a straight line. Since it is further from the physical cathode at lower current, it will approach the grid wires even closer, forming something close to a mirror image of the 0V potential contour. (This ignores the sideways velocity of the electrons. As far as I know the impact of this has never been analysed in detail, probably because the required computing power only appeared after the tube was considered obsolete). The extreme case of close spacing is the WE417A (or 5842), which achieves a record value of Gm for a small tube (25 mA/V) by very close construction. For this tube, at low currents the virtual cathode actually reaches the plane of the grid. From this point all of the classic mathematical description of triode operation becomes completely irrelevant.
From a practical point of view, at least as far as audio is concerned, the moral of all this is to operate tubes at as high a standing current and as low a bias level (i.e. closer to zero) as is possible for the circuit to operate correctly, so as to keep operation well into the 3/2 power part of the plate curves and hence reduce distortion, paticularly higher-harmonic distortion.
Most of the physics behind filamentary tubes is the same as for indirectly-heated tubes, but there are some differences. First, there is the question of the effective area of the cathode. An accepted formula for this is to use the length of the filament times twice the filament-grid distance [Spang48, p189].
The most significant difference arises because the voltage along the filament is not constant, but varies from one end to the other by the applied filament potential. Although this potential is small, it must be remembered that the effective plate voltage as seen at the cathode (filament) is also small. For example, a 300B operating under quiescent conditions of 350V and 90mA, with –60V on the grid, has a potential as seen at the cathode of around 15V, against a filament voltage of 5V. At the negative extreme of grid voltage, modulated by the signal, this effective voltage will drop close to or even below 5V.
When the effective plate voltage is less than the filament voltage, only part of the filament contributes to the plate current, i.e. the part which is still more negative than the filament. Furthermore, the current varies along the filament. The effect of this is that the current becomes dependent on the 5/2 power of the effective plate voltage, rather than the 3/2 power. As the plate voltage increases beyond the filament voltage, there is a gradual transition between the 5/2 power and the 3/2 power, which is approximately given by the formula [Dow37]:
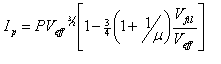 |
where: | P = perveance Veff = effective plate voltage Vfil = filament voltage |
It is this shift from a 3/2 law to a 5/2 law which explains the distinctive “tuck under” observed in the plate curves for filamentary tubes at high negative grid voltages and low currents. It has been observed [Bench99] that distortion can be measurably reduced with filamentary tubes by lowering the filament voltage to the lowest possible value consistent with avoiding saturation. In fact, in a filamentary tube with close cathode-grid spacing, at low currents the law will follow an even higher power, in theory 7/2.
Using AC rather than DC for the filaments does not reduce this effect. At any given instant, even with AC heating, there is a potential gradient along the filament (except of course for the moment when the filament voltage passes through zero). Some of the time it is greater than the equivalent DC voltage, and some of the time it is less, but taken through the whole AC cycle the net effect is essentially the same.
Any two different metals placed in contact with each other generate a potential difference. This is the underlying principle of all batteries, as well as the thermocouple. This difference is due to the different energy levels of the electrons in the two metals, and is called the contact potential of the two metals. The reasons are similar to the work function which determines electron emission, although the two are not the same. In fact, this effect applies even if the two metals are not in contact with each other, applying in this case to the electric field between them. Thus the grid and cathode of a tube, typically made of nickel and barium/strontium oxide respectively, have a small contact potential, which serves to change the effective grid potential. This contact potential is typically less than 0.5V.
The electrons must take a finite amount of time to travel from the cathode to the plate. This time is referred to as transit time, and is sometimes invoked to explain various phenomena relating to audio. Transit time did indeed become of practical importance when tubes were first used to build VHF and UHF equipment, and it ultimately sets a limit to the frequencies at which they can usefully operate (in the region 1-2GHz). The transit time can be calculated to be around 1nS from cathode to plate, which at audio frequencies is clearly not relevant.
The triode was the first amplifying device to be built, but at radio frequencies it suffers from a grave disadvantage because of the Miller Effect, which gives it a large effective input capacitance in the conventional common-cathode circuit. To avoid this, the tetrode was invented, having a second grid (the screen grid) between the triode grid (called the control grid in multi-grid tubes) and the plate. This grid is connected to a positive voltage close to the plate potential, but grounded to high frequencies through a decoupling capacitor. This results in an electrostatic shield which reduces the effective control grid-plate capacitance to a very low value.
A secondary effect of the screen grid is to reduce dramatically the influence of the plate voltage on the current flow, since the cathode is shielded from the plate by not one but two grids, and their screening effect is multiplied. As a result, the plate curves of a tetrode are very flat, as seen on the right-hand side of Figure 11. This corresponds to a very high value of plate resistance, as compared to a triode.
Some of the current from the cathode goes to the screen grid rather than the plate. The proportion depends on the shielding factor of the screen grid and on the relative potentials of the two electrodes, in much the same way as for a triode operated with a positive grid, and is typically 10-25%.
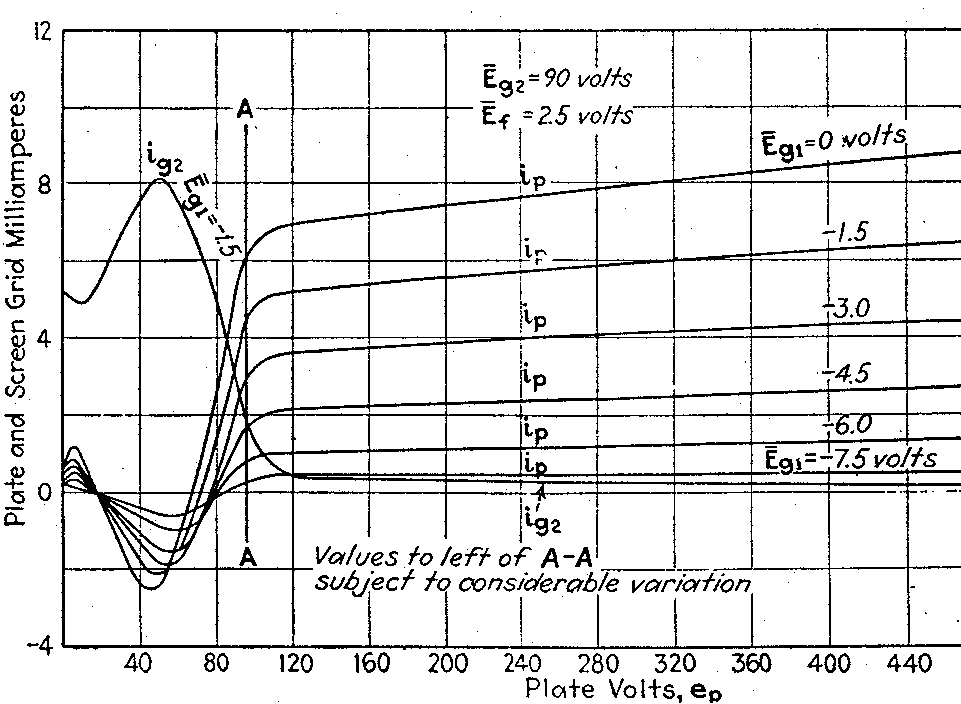 |
| Figure 11: Plate and screen grid current of true tetrode (UY224) |
Unfortunately the tetrode suffers from a severe problem in practice. The left-hand side of Figure 11 shows that at low plate voltages, the plate curves are extremely non-linear. This is because of secondary emission from the plate. When the screen grid voltage is higher than the plate, electrons emitted from the plate by secondary emission, as it is struck by the energetic primary electrons, are attracted back to the screen grid instead of returning to the plate as occurs in a triode. As a result, a tetrode can only be used if the circuit design is such that this part of the plate curve will not be encountered. For this reason, the simple tetrode has not been used, except for high-power transmitting tubes, since the 1930s. There has been no post-WWII small-signal tetrode produced in quantity.
The solution to the tetrode’s problem was to introduce a third grid between the screen grid and the plate. Called the suppressor grid, this is always connected to the cathode and hence appears negative both to the plate and to the screen grid. By this means, secondary electrons emitted from both of these electrodes see a field which sends them back where they came from, regardless of the relative potential between the electrodes. Thus the problems of secondary emission are eliminated. The suppressor grid has no effect on the flow of current, since by the time electrons reach it they have been sufficiently accelerated by the screen grid that they simply pass between the grid wires. They are slowed down but not stopped by the grounded suppressor grid.
Since the cathode is shielded from the plate by no less than three grids, the effect of plate voltage on current flow is negligible in the pentode, resulting in plate curves that are even flatter than for the tetrode.
The beam tetrode exploits an alternative way of avoiding secondary emission problems, without the manufacturing complexity of using a third grid. It was observed in the 1930s that if the distance from the screen grid to the plate is large enough, the space charge of the electrons flowing in this region can depress the potential substantially without having an actual electrode. This is the basis of the beam tetrode. The reduced potential in this region serves the same function as the suppressor grid, causing secondary electrons to turn back to their origin and avoiding their effect on the electrode currents.
To make this effect work in practice, three things are necessary. First, the electron flow must be confined to a narrow beam, otherwise the space charge spreads out parallel to the plate and the effect is lost. This is achieved by the beam electrodes, carefully shaped plates connected to the cathode and placed either side of the electron path between the screen grid and the plate. Second, the electrons must flow in clean “sheets”, which requires that the grid wires of the control grid and the screen grid be in line. This is not surprisingly a tricky manufacturing problem. Finally, the electrode dimensions and spacing must be carefully calculated.
Although there are slight differences in the detailed operation of pentodes and beam tetrodes, for most practical purposes they can be considered as the same. Indeed, there are tube types which some manufacturers built one way, and others in the other way. Eric Barbour [Barb97] mentions that the EL84/6BQ5 was made in both ways.
Of the many books which were written from 1920 into the 1950s about the theory of vacuum tubes, the two which are by a long way the most comprehensive are Spangenburg [Spang48] and Beck [Beck53]. Unfortunately these are extremely difficult to get hold of. These can really be regarded respectively as the US and UK “bible” on the subject. Spangenburg does however have a number of baffling minor errors in the transcription of formulae from other sources, which means that reference to original sources is required for certainty.
Dow [Dow37] seems to be easier to find, and gives many of the basic principles as well as a good introduction to the use of tubes in circuits. There is also a later book by Spangenburg [Spang57], although shorter than the first and covering semiconductors as well as tubes, which is quite adequate and seems easier to find. Reich [Reich41] is fairly basic but has the advantage of being available in a reprint [Reich95]. Valley & Wallman [Valley46] deals largely with DC and pulse amplifiers using tubes, and covers several topics such as low-level amplifiers in more detail than elsewhere. Mitchell [Mitch93] gives the most comprehensive tube data available, unfortunately only for a small selection of tube types. Smullin [Smullin59] gives a comprehensive treatment of all aspects of noise in vacuum tubes.
| [Barb97] | Barbour E., EL84: The Baby With Bite, Vacuum Tube Valley issue 8, 1997 |
| [Beck53] | Beck A.H.W., Thermionic ValvesCambridge University Press, 1953 |
| [Bench99] | Bench S., Directly Heated Triodes operated with lower voltage on the filaments, available at http://members.aol.com/sbench102/dht.html |
| [Chaff33] | Chaffee E.L., Theory of Thermionic Vacuum Tubes, McGraw-Hill, 1933 |
| [Dow37] | Dow W.G., Fundamentals of Engineering Electronics, Wiley, 1937 |
| [Frem39] | Fremlin J.H., Calculation of Triode Constants, Electrical Communications, July 1939 |
| [Lang23] | Langmuir I., The Effect of Space Charge and Initial Velocities on the Potential Distribution and Thermionic Current Between Parallel Plane Electrodes, Physics Review vol. 21 pp419-435, 1923 |
| [Lang53] | Langford-Smith F., Radiotron Designer’s Handbook, Iliffe, 1953 |
| [Max71] | Maxwell J.C., A Treatise on Electricity and Magnetism, 1871, reprinted by Dover Publications, 1954, ISBN 0-486-60636-8 |
| [Mitch93] | Mitchell T., The Audio Designer’s Tube Register, Media Concepts, 1993, ISBN 0-9628170-1-5 |
| [Reich41] | Reich H.J., Principles of Electron Tubes, Wiley, 1941 |
| [Reich95] | Reich H.J., Principles of Electron Tubes, reprinted by Audio Amateur Press, 1995, ISBN 1-882580-07-9 |
| [Smullin59] | Smullin L.D. & Haus H.A., Noise in Electron Devices, MIT Press, 1959 |
| [Spang48] | Spangenburg K.R., Vacuum Tubes, McGraw-Hill, 1948 |
| [Spang57] | Spangenburg K.R., Fundamentals of Electron Devices, McGraw-Hill, 1957 |
| [Valley46] | Valley G.E. & Wallman H., Vacuum Tube Amplifiers, MIT Press, 1946, reprinted by Boston Technical Publishers Inc., 1964 |
Revision 2, 2 January 2002.